Time-Lapse Auralization of
Ocean Waves
Ward Cunningham
September 24, 2004
Revison 4, January 31, 2006
Mechanical waves propagate because of differential interaction between kinetic and potential energy. Despite differences in the mass, force and motion of their constituent materials, both sound waves and ocean waves propagate energy such that distinct sources can be resolved by a distant observer. In this work I take observations collected at the sea surface by buoy and transform them so that they can be rendered as stereophonic sound. The transformation is primarily one of time scaling, converting days to seconds, but also includes projection from three dimensions into two and filtering to balance spectral response. I conclude with a subjective description of the sounds produced and directions for reproducing the same sounds on a personal computer.
Data Collection
I became interested in the properties of ocean waves while staying as a guest of Mr. and Mrs. Hofmann at their beach house high on a bluff overlooking the rugged shoreline of the Oregon coast in 1975. Although still a graduate student at the thoroughly landlocked Purdue University, my stay with the Hofmann's was informed by the copy of Willard Bascom's Waves and Beaches which I'd picked up on a day trip to Oregon's Marine Science Center in Newport. This book described his own study of the interaction of surf and sand conducted during world war two in preparation for the Normandy invasion. Bascom also described the tremendous energy carrying capacity
of huge long period swell with its sources as far away as the other
hemisphere.
invasion. Bascom also described the tremendous energy carrying capacity
of huge long period swell with its sources as far away as the other
hemisphere. I remained interested in wave dynamics and developed the notion of auralization, as an analogy to computer visualization, through thought experiments on subsequent visits to the coast. Usually my thoughts involved variations on data collection apparatus that I might build and maintain if I only had a beach house of my own. Then came the internet. While corresponding with Anthony Tekatch, author of the Electromagnetic Radiation Spectrum Poster, suggesting he add ocean waves at a frequency of 0.1 Hz, I sought a current reference and located by web search Chapter 16 of Robert H. Stewart's Introduction to Physical Oceanography. Correspondence with Dr. Stewart then lead me to the Coastal Data Information Program (CDIP) and the able assistance of Julie Thomas who suggested I look at their online data from buoy stations 029 and 071, their two in deepest water, 550 meters.
These stations use Datawell directional buoys that float on the water's surface recording motion in all three dimensions which it transmits to nearby shore stations by radio. CDIP collects, analyzes, reports and archives data from these and many other sensors and sensor types. They make all of this available through an interactive web interface and through cgi scripts. The products I found most useful were:
- "Mountain" style monthly plots for locating periods of interesting activity. These are time-energy-frequency plots generated on demand from the interactive interface.
- Datawell Timeseries
in the xy file format which I could easily download and process on my
own computer. These consist of time and x, y, z displacement records
recorded at slightly faster than one a second.
for mo in 01 02 03 04 05 06 07 08 09 10 11 12This attempts to retrieve data for some bogus dates, like Feb 31, and for dates for which data is not available. The result was an 11-byte file containing an error messages which I remove with this shell script:
do
for da in 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
do
curl http://cdip.ucsd.edu/data_access/justdar.cdip?029+xy+2004$mo$da >2004$mo$da
done
done
rm `find . -size 11c`
The returned files had data
records with interspersed header records before every thirty minutes of
data. I read this using the following Python script:
A variety of sound recording formats exist for personal computers. I chose the widely understood "wav" format which is conveniently supported by the standard Python wave module. I recorded at the CD standard sampling rate of 44,100 Hz. Subjectively, half that sampling rate would be preferable as it moves typical sounds closer to the middle of the hearing range and makes for smaller files too. I chose to effect the same shift by simply doubling recording samples retrieved from the buoy data.
The water molecules, who's motion makes for ocean waves, travel in a circular path with a maximal diameter equal to the horizontal crest to crest dimension of the wave. This means that long period, low frequency ocean waves move a lot more water than smaller, higher frequency waves. For this reason I chose to emphasize lower frequencies by applying digital filtering to the data samples as I transfered them. I used a first-order filter, similar to an RC filter, with a time constant substantially longer than my lowest frequency. I applied this filter after doubling wave samples so the doubled samples are not likely identical.
Auditory pathways in the human brain combine signals arriving at both ears and, through comparisons of both amplitude and phase, construct a sense of direction to the source. Stereophonic sound exploits this processing by recording music (for example) with multiple microphones and mixing those signals into two independent speaker channels. That is, the signals represent the sound near the source. Alternately, binaural sound is recorded near the listener, normally with the aid of a dummy head, and produces two independent channels that are best listened to with headphones.
It may be possible to construct stereophonic signals from multiple, time synchronized buoys. However, the horizontal directionality of single buoy recordings makes a binaural approximation the more convenient.
I neglected the z component of the x, y, z data reasoning that it was present in the x and y components already (due to the circular motion of water molecules) and it carried no directional information. I then modeled the "dummy head" as a detector facing in a specific compass direction and with ear cavities capable of detecting motion only along a perpendicular to an "ear drum" oriented with positive or negative displacement on the order of 30 degrees from the direction the "head" faced.
I added the binaural modeling and found that I could get only the most general sense of where each hiss was located. However,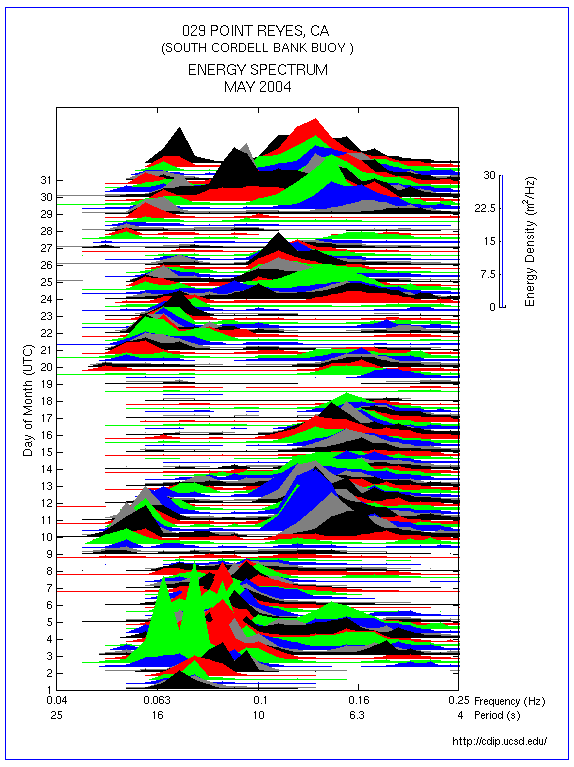 I immediately recognized several shorter
lived and narrowly spread hiss components that would appear briefly to
one side or another or even dart across my aural "field of view".
I immediately recognized several shorter
lived and narrowly spread hiss components that would appear briefly to
one side or another or even dart across my aural "field of view".
I suspect that an improved dummy head model will increase the position resolvability of the stronger components. These are often over an octave wide which makes them percieved as general noise. Modeling options include included simulating some ear separation so that phase disparity of off-axis results. Finally, some spectral coloring modeling that applied by the head and outer ear will offer the brain more directional queues.
I found the first 19 days of May to be a conveniently sized dataset identified by the file pattern, 200405[01]*. I make available the uncompressed wav file and mp3 equivalent for this data. Download the file here:
In the coming months I will be auralizing more datasets from more sites and seasons. I will explore various compression algorithms so that these results are more easily distributed over the web. I'll be improving my binaural model and may try to correlate my results with satellite weather loops.
Jim Besemer and Kevin Altis helped me many times with Python programming. Jim sent me a program that generated a quarter-second beep. This grew into the auralizer. Kevin introduced me to Python and stood by online as I struggled to get beyond my first half-second of hiss.
My colleagues, David Trowbridge and Larry Brader feined interest as I worked on the program during free moments on a conference trip. Thanks guys. And thank you to my wife Karen who put up with me playing wav loops through the family stereo for hours to see what else I could hear.
While he was working for CDIP Bob Sturm did a similar study, but with quite different results. Here is a page with some of his links and sound examples. See also an online publication or this paper: Sturm, Bob L. "Pulse of an Ocean: Sonification of Ocean Buoy Data." Leonardo Journal of Arts and Sciences, 38(2), 2005.
The STEREO/IMPACT project distributes application programs that they use for sonification of space "weather" and similar applications within the "Sounds of Space" program.
© 2004
stdin = os.fdopen(0)My normal mode of exploration was to "cat" together multiple days of buoy data selected by shell wildcard expressions and "pipe" that into a python processing program using the above reader. For large runs the processing time can be substantial so I print selected header records as a progress indicator.
for line in stdin:
if line[0].isdigit():
data = line.split()
x = int(data[1])
y = int(data[2])
...
elif line.startswith("Start time"):
print line,
Signal Processing
Human hearing runs from about 20 Hz to 20,000 Hz. Ocean waves run from about 0.05 Hz to 0.25 Hz. To hear ocean waves as sound they need to be sped up by a factor of 10,000. This turns out to be a trivial operation with the computer for the simple reason that typical sampling rates have already been chosen so that both frequency ranges fall well below the Nyquist cut-off frequency for the signals in question. An appropriate speedup can be achieved by equating one ocean wave sample to one digital sound sample.A variety of sound recording formats exist for personal computers. I chose the widely understood "wav" format which is conveniently supported by the standard Python wave module. I recorded at the CD standard sampling rate of 44,100 Hz. Subjectively, half that sampling rate would be preferable as it moves typical sounds closer to the middle of the hearing range and makes for smaller files too. I chose to effect the same shift by simply doubling recording samples retrieved from the buoy data.
The water molecules, who's motion makes for ocean waves, travel in a circular path with a maximal diameter equal to the horizontal crest to crest dimension of the wave. This means that long period, low frequency ocean waves move a lot more water than smaller, higher frequency waves. For this reason I chose to emphasize lower frequencies by applying digital filtering to the data samples as I transfered them. I used a first-order filter, similar to an RC filter, with a time constant substantially longer than my lowest frequency. I applied this filter after doubling wave samples so the doubled samples are not likely identical.
p = .99Ocean waves from different sources and traveling in different directions can pass by each other without further interaction. This holds so long as the summing of wave heights is linear: that is, the waves don't break or collide with submerged obstacles including the ocean floor. It has been the possibility of perceiving the source of waves as stereophonic sound that has motivated my curiosity over the years. Now, the remaining element of required signal processing is to convert x, y, z data into left and right stereo channels.
lf = p * lf + (1 - p) * left
rf = p * rf + (1 - p) * right
Auditory pathways in the human brain combine signals arriving at both ears and, through comparisons of both amplitude and phase, construct a sense of direction to the source. Stereophonic sound exploits this processing by recording music (for example) with multiple microphones and mixing those signals into two independent speaker channels. That is, the signals represent the sound near the source. Alternately, binaural sound is recorded near the listener, normally with the aid of a dummy head, and produces two independent channels that are best listened to with headphones.
It may be possible to construct stereophonic signals from multiple, time synchronized buoys. However, the horizontal directionality of single buoy recordings makes a binaural approximation the more convenient.
I neglected the z component of the x, y, z data reasoning that it was present in the x and y components already (due to the circular motion of water molecules) and it carried no directional information. I then modeled the "dummy head" as a detector facing in a specific compass direction and with ear cavities capable of detecting motion only along a perpendicular to an "ear drum" oriented with positive or negative displacement on the order of 30 degrees from the direction the "head" faced.
left = leftSin * x + leftCos * yI experimented with a variety of displacements and found 30 degrees to produce good separation for most signal components.
right = rightSin * x + rightCos * y
Subjective Assessment of Results
I selected the month of May, 2004 for my initial tests because the "mountain" plots for the Point Reyes Buoy (029) showed strong and varied frequency components for this interval. Short runs which compressed 12 hours of data into about a second of sound were disappointing because the result was a hiss without variation. Longer runs produced a gracefully evolving hiss but no distinctly identifiable sources. I added sample doubling and low pass filtering with the result that I could identify separately evolving hisses. A given hiss would slowly drift up in frequency while another would get stronger or drift down.I added the binaural modeling and found that I could get only the most general sense of where each hiss was located. However,
 I immediately recognized several shorter
lived and narrowly spread hiss components that would appear briefly to
one side or another or even dart across my aural "field of view".
I immediately recognized several shorter
lived and narrowly spread hiss components that would appear briefly to
one side or another or even dart across my aural "field of view". I suspect that an improved dummy head model will increase the position resolvability of the stronger components. These are often over an octave wide which makes them percieved as general noise. Modeling options include included simulating some ear separation so that phase disparity of off-axis results. Finally, some spectral coloring modeling that applied by the head and outer ear will offer the brain more directional queues.
I found the first 19 days of May to be a conveniently sized dataset identified by the file pattern, 200405[01]*. I make available the uncompressed wav file and mp3 equivalent for this data. Download the file here:
In the coming months I will be auralizing more datasets from more sites and seasons. I will explore various compression algorithms so that these results are more easily distributed over the web. I'll be improving my binaural model and may try to correlate my results with satellite weather loops.
Acknowledgments
I would first like to thank those parties mentioned in the Data Collection section of this paper. This work by a curious amateur would not be possible without their willingness and energy making scientific resources available online. Reinhard Flick was an important conduit while I made the connection with CPID and offered back of the envelope calculations and other encouragement along the way. Bill O'Reilly accepted our cc's without complaint. Both figures in this report are due to CPID.Jim Besemer and Kevin Altis helped me many times with Python programming. Jim sent me a program that generated a quarter-second beep. This grew into the auralizer. Kevin introduced me to Python and stood by online as I struggled to get beyond my first half-second of hiss.
My colleagues, David Trowbridge and Larry Brader feined interest as I worked on the program during free moments on a conference trip. Thanks guys. And thank you to my wife Karen who put up with me playing wav loops through the family stereo for hours to see what else I could hear.
Links
San Francisco's Exploratorium offers this online exhibit that will demonstrate, with headphones, spatial separation of multiple complex sounds.While he was working for CDIP Bob Sturm did a similar study, but with quite different results. Here is a page with some of his links and sound examples. See also an online publication or this paper: Sturm, Bob L. "Pulse of an Ocean: Sonification of Ocean Buoy Data." Leonardo Journal of Arts and Sciences, 38(2), 2005.
The STEREO/IMPACT project distributes application programs that they use for sonification of space "weather" and similar applications within the "Sounds of Space" program.
© 2004