Theoretical Speedup Limit +
Paul E. McKenney
Sequent Computer Systems, Inc.
Copyright (c) 1995, Paul E. McKenney
All rights reserved
Synchronization primitives allow controlled coordination of different activities on a multiprocessor system. The only reason to go to the trouble of parallelizing a program is to gain performance, so it is necessary to understand the performance implications of synchronization primitives in addition to their correctness, liveness, and safety properties.This paper presents a set of patterns for the use of a simple set of synchronization primitives to increase performance or reduce maintenance costs of parallel programs running on symmetric shared-memory multiprocessors.
Section sec:example presents the example that is used throughout the paper to demonstrate use of the patterns. Section sec:parallel describes the overall parallelization pattern, and the succeeding sections describe subpatterns of this pattern.
A simple hashed lookup table is used to illustrate the patterns in this paper. This example searches for a specified key in a list of elements and performs operations on those elements. Both the individual elements and the list itself may require mutual exclusion.
The data structure for a mono-processor implementation is shown in Figure fig:lkupstruct.
typedef struct locktab {
struct locktab_t *rc_next;
int rc_key;
int rc_data;
} locktab_t;
Lookup-Table Element
+
Again, this structure will be embellished as needed for each of the example uses with synchronization.
A search for the element with a given key might be implemented as shown in Figure fig:lkupsrch.
/* Header for list of locktab_t's. */Lookup-Table Search +locktab_t *looktab_head[LOOKTAB_NHASH] = { NULL }; #define LOOKTAB_HASH(key) \ ((key)
/* * Return a pointer to the element of the * table with the specified key, or return * NULL if no such element exists. */
locktab_t * locktab_search(int key) { locktab_t *p;
p = locktab_head[LOOKTAB_HASH(key)]; while (p != NULL) { if (p->rc_key > key) { return (NULL); } if (p->rc_key == key) { return (p); } p = p->rc_next; } return (NULL); }
Speedup: Getting a program to run faster is the only reason to go to all of the time and trouble required to parallelize it. Speedup is defined to be the ratio of the time required to run a sequential version of the program to the time required to run a parallel version.
Contention: If more CPUs are applied to a parallel program than can be kept busy given that program, the excess CPUs are prevented from doing useful work by contention.
Overhead: A monoprocessor version of a given parallel program would not need synchronization primitives. Therefore, any time consumed by these primitives is overhead that does not contribute directly to the useful work that the program is intended to accomplish. Note that the important measure is usually the relationship between the synchronization overhead and the serial overhead--the greater the serial overhead of a given critical section, the greater the amount of synchronization overhead that may be tolerated.
Read-to-Write Ratio: A data structure that is mostly rarely updated may be protected with lower-overhead synchronization primitives than may a data structure with a high update rate.
Economics: Budgetary constraints can limit the number of CPUs available regardless of the potential speedup.
Development and Maintenance Costs: Budgetary constraints can limit the number and types of modifications made to an existing program -- a given degree of speedup is worth only so much time and trouble.
Note that these forces may also appear as part of the context. For example, economics may act as a force (``cheaper is better'') or as part of the context (``the cost must not exceed \$100'').
Appendix sec:forcerelate presents mathematical relationships between these forces. An understanding of these relationships can be very helpful when resolving the forces acting on an existing parallel program. The following gives a brief summary of these relationships:
relate Relationship Between Subpatterns of Parallel Pattern +
There are many other parallel-programming performance patterns:\footnote{ Operation combining, optimistic locking, spin versus block, wait-free synchronization, and data layout, to name but a few. } any attempt to capture all of them in a single paper would be as foolhardy as an attempt to capture all data-structure-related patterns in a single paper.
The arcs in Figure fig:relate correspond to transformations between the subpatterns:
A Parallelize an existing sequential program. This increases speedup, but the increase will be limited by contention and overhead. In addition, parallelization usually increases maintenance costs.
B Serialize a parallel program. This decreases maintenance costs, but also eliminates speedup.
C Insert explicit locking into a parallel program that previously relied on data ownership. This increases overhead, thereby decreasing speedup.
This action might nevertheless be warranted when maintaining a parallel version of a serial third-party product--a new version of the product might incorporate changes that invalidate the assumptions on which the data ownership rested.
The effect is to give up some speedup in return for reduced maintenance costs (the more heavily a third-party product is modified, the greater the maintenance costs).
D Partition a data structure so that individual CPUs own portions of it, eliminating the need for explicit locking and its overhead thereby increasing speedup.
E Combine partitioned critical sections. This can increase speedup on systems with very high synchronization-primitive overhead, but will normally decrease speedup. The simpler code-locking paradigm often results in decreased maintenance costs.
F Partition code-locked critical sections. This usually increases speedup, but may also increase maintenance costs.
G Split up fused critical sections. If the overhead of the synchronization primitives is low compared to that of the code making up the critical section, this will increase speedup. This action can be motivated when moving the program to a machine with cheaper synchronization primitives.
H Fuse critical sections. If the overhead of the synchronization primitives is high compared to that of the code making up the critical section, this will increase speedup.
I,L,M Use reader/writer locking. If the critical sections have high overhead compared to that of the synchronization primitives, if there is a high read-to-write ratio, and if the existing program has high contention, this will increase speedup.
J,K,N Stop using reader/writer locking. Since reader/writer primitives often have higher overhead than do normal synchronization primitives, this action will result in greater speedup if the read-to-write ratio or the contention level is too low for reader/writer primitives to be effective.
The required speedup may be modest, or the contention and overhead present may be negligible, thereby allowing adequate speedups.
Economics may prohibit applying more than a small number of CPUs to a problem, thereby rendering high speedups irrelevant.
Development and maintenance costs of highly-parallel code might be prohibitive.
Therefore, code locking should be used on programs that spend only a small fraction of their run time in critical sections or from which only modest scaling is required. In these cases, the simplicity of code locking will result in much lower development costs being incurred while parallelizing.
The lookup-table example could be used verbatim, but calls to locktab_search() function and subsequent uses of the return value would have to be surrounded by a synchronization primitive as shown in Figure fig:codelock.
Code-Locking Lookup Table +/* * Global lock for locktab_t * manipulations. */
slock_t locktab_mutex;
. . .
/* * Look up a locktab element and * examine it. */
S_LOCK(&locktab_mutex); p = locktab_search(mykey);
/* * insert code here to examine or * update the element. */
S_UNLOCK(&locktab_mutex);
Note that the lock must be held across the use of the element as well as across the lookup, particularly if the element can be deleted. This means that it is not useful to bury the locking in locktab_search() itself.
Nevertheless, it is relatively easy to create and maintain a code-locking version of a program. No restructuring is needed, only the (admittedly non-trivial) task of inserting the locking operations.
This program would scale well if the table search and update was a very small part of the program's execution time.
A greater speedup than can be obtained via code locking must be needed badly enough to invest the development, maintenance, and machine resources required for more aggressive parallelization.
The program must also be partitionable so as to allow partitioning to be used to reduce contention and overhead.
Many algorithms and data structures may be split into independent parts, with each part having its own independent critical section. Then the critical sections for each part could execute in parallel (although only one instance of the critical section for a given part could be executing at a given time). This partitioning is useful in Regime 3 of Figure fig:overhead, where critical-section overhead must be reduced. Partitioning reduces this overhead by distributing the instances of the overly-large critical section into multiple critical sections. This reduces $n_c$ in Equation eq:overhead, thereby reducing $T_c$ and increasing the speedup, as can be seen from Figures fig:speedup, fig:cpulim, and fig:cpueff.
For example, if there were several independent lookup tables in a program, each could have its own critical section, as shown in Figure fig:partition. This figure assumes that locktab_search() has been modified to take an additional pointer to the table to be searched. Structuring the code in this manner allows searches of different tables to proceed in parallel, although searches of a particular table will still be serialized.
Partitioned Lookup Table +/* Global lock for locktab_t manipulations. */
slock_t my_locktab_mutex[LOCKTAB_NHASH];
. . .
/* Look up a locktab element and examine it. */
S_LOCK(&my_locktab_mutex[LOCKTAB_HASH(mykey)]); p = locktab_search(my_locktab, mykey);
/* insert code here to examine or update the element. */
S_UNLOCK(&my_locktab_mutex[LOCKTAB_HASH(mykey)]);
Locating the lock for each hash line in the hash-line-header data structure, as shown in Figure fig:datalock, results in a special case of partitioning known as ``data locking''. This may be done if the individual elements in a table are independent from one another, and allows searches of a single table to proceed in parallel if the items being searched for do not collide after being hashed.
Data Locking +/* * Type definition for locktab header. * All fields are protected by lth_mutex. */
typedef struct locktab_head { locktab_t *lth_head; slock_t *lth_mutex; } locktab_head_t;
/* Header for list of locktab_t's. */
locktab_head_t *looktab_head[LOCKTAB_NHASH] = { NULL }; #define LOCKTAB_HASH(key) ((key)
/* * Return a pointer to the element of the table with the * specified key, or return NULL if no such element exists. */
locktab_t * locktab_search(int key) { locktab_t *p;
p = locktab_head[LOCKTAB_HASH(key)].lth_head; while (p != NULL) { if (p->rc_key > key) { return (NULL); } if (p->rc_key == key) { return (p); } p = p->rc_next; } return (NULL); }
/* . . . */
/* Look up a locktab element and examine it. */
S_LOCK(&locktab_head[LOCKTAB_HASH(key)].lth_mutex); p = locktab_search(mykey);
/* insert code here to examine or update the element. */
S_UNLOCK(&locktab_head[LOCKTAB_HASH(key)].lth_mutex);
These two techniques can be combined to allow parallel searching within and between lookup tables.
In this case, data locking is not too much more complex than code locking. Programs containing data structures that are not fully independent are much more challenging; such programs must be restructured in order to get the needed independence or must use complex locking models that allow near-independence to be exploited. However, in the second example, once the transformation to data locking is completed, the speedup may be increased simply by increasing the size of the hash table.
The program must be perfectly partitionable, eliminating contention an synchronization overhead.
If each key class can be assigned to a separate process, we have a special case of partitioning known as data ownership. Data ownership is a very powerful pattern, as it can entirely eliminate synchronization overhead ($d_c$ becomes zero in Equation eq:overhead). This is particularly useful in cases in Regime 1 in Figure fig:overhead that have small critical sections whose overhead is dominated by synchronization overhead. If the key classes are well balanced, data ownership can allow virtually unlimited speedups.
Partitioning the lookup-table example over separate processes would require a convention or mechanism to force lookups for keys of a given class to be performed by the proper process. Such a convention or mechanism would be application and implementation specific, and beyond the scope of this paper. However, a data-ownership partitioning for a parallel memory allocator with partially-independent data structures is described by McKenney and Slingwine McKenney93.
Synchronization overhead must dominate, and contention must be low enough to allow increasing the size of critical sections.
For example, imagine a program containing back-to-back searches of a code-locked lookup table. A straightforward implementation would acquire the lock, do the first search, do the first update, release the lock, acquire the lock once more, do the second search, do the second update, and finally release the lock. If this sequence of code was dominated by synchronization overhead, eliminating the first release and second acquisition as shown in Figure fig:fuse would increase speedup.
Critical-Section Fusing +/* * Global lock for locktab_t * manipulations. */
slock_t locktab_mutex;
. . .
/* * Look up a locktab element and * examine it. */
S_LOCK(&locktab_mutex); p = locktab_search(mykey);
/* * insert code here to examine or * update the element. */
p = locktab_search(myotherkey);
/* * insert code here to examine or * update the element. */
S_UNLOCK(&locktab_mutex);
Synchronization overhead must not dominate, contention must be high, and read-to-write ratio must be high. Low synchronization overhead is especially important, as most implementations of reader/writer locking incur greater synchronization overhead than does normal locking.
Specialized forms of reader/writer locking may be used when synchronization overhead dominates Andrews91 Tay87.
The lookup-table example uses read-side primitives to search the table and write-size primitives to modify it. Figure fig:rwrdlock shows locking for search, and Figure fig:rwwrlock shows locking for update. Since this example demonstrates reader/writer locking applied to a code-locked program, the locks must surround the calls to locktab_search() as well as the code that examines or modifies the selected element.
Reader/writer locking can easily be adapted to partitioned parallel programs as well.
Read-Side Locking +/* * Global lock for locktab_t * manipulations. */
srwlock_t locktab_mutex;
. . .
/* * Look up a locktab element and * examine it. */
S_RDLOCK(&locktab_mutex); p = locktab_search(mykey);
/* * insert code here to examine * the element. */
S_UNLOCK(&locktab_mutex);
Write-Side Locking +/* * Global lock for locktab_t * manipulations. */
srwlock_t locktab_mutex;
. . .
/* * Look up a locktab element and * examine it. */
S_WRLOCK(&locktab_mutex); p = locktab_search(mykey);
/* * insert code here to update * the element. */
S_UNLOCK(&locktab_mutex);
I owe thanks to Ward Cunningham and Steve Peterson for encouraging me to set these ideas down. I am indebted to Dale Goebel for his consistent support.
The forces acting on the performance of parallel programs are speedup, contention, overhead, economics, and development and maintenance costs. Of these, speedup, contention, overhead, read-to-write ratio, and economics have strong mathematical interrelationships.
Consider an idealized parallel program with a single critical section, and where all code outside the critical section may be executed with an arbitrarily fine granularity.\footnote{ In real life, performance penalties must be paid for too-fine granularity, resulting in speedup limitations. In addition, data dependencies can result in additional limitations. This idealized model nevertheless produces several widely-applicable rules of thumb.} Only one CPU may execute in the critical section at a given time, and thus at most one CPUs worth of throughput may be obtained from that critical section. This effect is known as ``Amdahl's Law'', and may be cast into mathematical form as follows:
S < \frac{1}{T_c} +
where $S$ is the maximum speedup obtainable and $T_c$ is the fraction of total time spent in the critical section, including the overhead of the mutual-exclusion primitive. This expression can be roughly adapted for programs containing multiple independent critical sections by setting $T_c$ equal to the maximum of the times spent in the critical sections.\footnote{ An analogy to queuing systems can provide more accurate results. Contention is analogous to in-queue waiting time, overhead and critical-section execution time are analogous to service rate, and attempts to enter the critical section are analogous to arrival rate.}
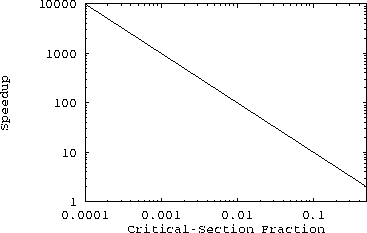
A plot of Equation eq:speedup is shown in Figure fig:speedup.

Theoretical Speedup Limit
+
The combined forces of contention and overhead will always force a program's speedup to be below the line in this plot: a program that spends 25% of its time in its critical section cannot achieve a speedup of greater than four.
The next force, economics, manifests itself as a constraint on speedup. This paper looks at two simple economic constraints: (1) a budgetary limit on the number of CPUs, and (2) a cost-effectiveness constraint that requires that at least some fraction of the last CPU's capacity be used for useful work.
The first constraint limits the number of available CPUs $n$:
S_{e1} = \frac{1}{\frac{1 - T_c}{n} + T_c}
This equation simply divides the parallelizable fraction of the work ($1 - T_c$, assuming negligible synchronization overhead) by the available number of CPUs, adds the serial fraction and takes the reciprocal to calculate the speedup. Rearranging:
S_{e1} = \frac{n}{1 + (n - 1) T_c} +
This expression is plotted on Figure fig:cpulim for $n$ equal to 10, 100, and 1000.

Speedup Given Limited CPUs
+
The straight line on this plot is the theoretical speedup given unlimited numbers of CPUs. Contention and overhead force a program's speedup to be below this line, while economics forces it even further below, depending on the number of CPUs available.
The second constraint places a lower bound on the marginal speedup obtained by adding an additional CPU. The marginal speedup is calculated by subtracting the speedup attained by $n-1$ CPUs from that attained by $n$ CPUs:
m = \frac{n}{1 + (n - 1) T_c} - \frac{n - 1}{1 + (n - 2) T_c}
Solving this equation for $n$ gives the maximum number of CPUs that may be added while still beating a specified marginal speedup $m$:
n = \frac{\sqrt{m^2 T_c^2 - 4 m T_c + 4 m} + 3 m T_c - 2 m}{2 m T_c}
Substituting this CPU limit into Equation eq:speedupe1 (and thus once again assuming that synchronization overhead is negligible):
S_{e2} = \frac{\sqrt{m T_c^2 - 4 T_c + 4} + 3 T_c \sqrt{m} - 2 \sqrt{m}} {T_c \sqrt{m T_c^2 - 4 T_c + 4} + T_c^2 \sqrt{m}}
This equation is plotted for marginal speedups of 0, 0.5, 0.7, and 0.9 in Figure fig:cpueff.

Speedup Given Marginal Speedup Constraint
+
Again, contention and overhead force a program's speedup to be below the speedup-0 line, while economics forces it even further below, depending on the number of CPUs available.
The common thread through all of the speedup plots is that minimizing $T_c$ leads to high speedups. The $T_c$ term can be broken down into critical-section and synchronization overhead components as follows:
T_c = n_c (d_c + d_p) +
where $n_c$ is the number of times per unit time that the critical section was entered, $d_c$ the critical-section overhead, and $d_p$ the synchronization overhead. Figure fig:overhead shows a plot of $T_c$ versus $d_c$ for $n_c = 1$ and $d_p = 0.001$.

Critical-Section Overhead Regimes
+
This plot shows three regimes: the first (below 0.0002) dominated by the synchronization overhead $d_p$, the second (from 0.0002 to 0.003) where both have influence, and the third (above 0.003) dominated by the critical-section overhead $d_c$.
Synchronization overheads can be quite large in comparison to critical-section overheads. For example, the Stanford Flash project plans to produce a machine with $d_p$ equal to about one to two microseconds but with $d_c$ as low as a few nanoseconds Heinrich94 so that synchronization overhead can be over two orders of magnitude greater than critical-section overhead. Critical sections guarding simple single-variable updates on the Flash therefore fall on the extreme left of Figure fig:overhead: maximum speedups are determined in this case by the overhead of the synchronization primitives. The high cost of general-purpose synchronization operations relative to machine instructions is likely to persist for the foreseeable future Hennessy91 Stone91
Note also that there is nothing stopping $T_c$ from being greater than one, in which case the theoretical speedup with be less than one. This simply means that the parallelism present in the implementation is not sufficient to overcome the synchronization overhead. Many projects, both in academia and industry, have experienced this frustrating situation.
Reader/writer primitives are helpful in cases where the overhead of the critical section dominates that of the primitives and where the read-to-write ratio is high. The derivations in this section will use the fraction of operations that require write-side locking $f_w$ in place of the more intuitive read-to-write ratio.
The speedup due to use of reader/writer locking can be approximated as follows:
S = f_w + (1 - f_w) \min(n, \frac{1 - f_w}{f_w})
where $n$ is the number of CPUs. This approximation assumes that readers and writers alternate access to the data structure: one writer proceeds through its critical section, then all readers proceed, then the next writer proceeds, and so on. It also assumes that the overhead of the reader and writer critical sections are constant and identical. More sophisticated analyses may be found in the literature Reiman91.
A plot of this expression is shown in Figure fig:rwlock.
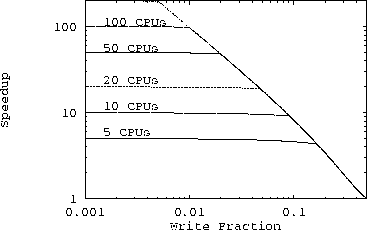
Reader/Writer Locking Speedup
+
As can be seen from this figure, reader/writer locking can achieve nearly linear speedups if the write fraction is low enough (i.e., if the read-to-write ratio is high enough).
The following sections examine ways to increase speedups by reducing contention and overhead. Although methods of removing economic constraints lie beyond the scope of this paper, reductions in contention and overhead can result in more effective use of limited resources.