I picked up a neat toy. It's a pendulum that swings from what looks vaguely
like an eight inch high hangman's gallows. The pendulum has a magnet on
the end that swings over a field of additional magnets stuck to the metal
base. With two or more magnets the base the trajectory of the
pendulum becomes chaotic.
It's a joy to watch. But after a while I wanted to understand it more. So I wrote a little pendulum simulator. I start by integrating acceleration (a) to get velocity (v), then integrating it to get position (p).
p := 200 @ 200. v := 0.01 @ 0.
4000 timesRepeat: [v := p + a. p := p + v]
Inside this loop I set acceleration to be the sum of forces from a collection of magnets (m). Each magnet (e) applies a force in direction (d) which I scale inversely by the square of the distance to the magnet.
m := Array with: 300 @ 200 with: 200 @ 300 with: 400 @ 300.
a := m inject: 0@0 into: [:s :e | d := e - p. s + (d / d r squared)]
Now, to render the behavior of this simulation, I draw a series of polygons
bounded by four vertices (p1 - p4). With each simulation step I advance
the polygon by moving the leading edge (p1 p2) into the trailing edge (p3
p4) and computing a new leading edge (q +/- r) as a function of simulated
position and velocity.
q := p rounded r := (10 * v transpose) rounded. p3 := p2. p4 := p1. p1 := q - r. p2 := q + r.
These polygons are rendered a GraphicsContext (gc) in yellow. Two sides of the polygon are emphasized in black to complete the effect.
gc paint: ColorValue yellow; displayPolygon: (Array with: p1 with: p2 with: p3 with: p4); paint: ColorValue black; displayLineFrom: p4 to: p1; displayLineFrom: p3 to: p2.
Here is the workspace contents I used to run this program VisualWorks 2.5. Interesting variations you might try include new initial conditions, more or different magnets, changing the power of the inverse square to fractional numbers like 1.8 or 2.2, and, rendering different variables or the same variables differently.
(four years pass)
Plan B is Morphic. Morphs are shapes that are easily manipulated with assorted mouse clicks. Once I learned these, especially Alt-Left-Click, the Morphic secret weapon, I could play with and learn a few dozen of the hundred morphs already present. I used AtomMorph as a guiding example. Like it, my new morph would refine ElipseMorph so that rendering would be taken care of. I used plain old ellipses as the magnets that my new morph would respond to each time Morphic asked it to step. Here is the step code.
step
| magnets acceleration delta |
super step.
mags := owner submorphs select:
[:each | each class == EllipseMorph].
acceleration := magnets inject: 0@0 into:
[:sum :each |
delta := each position - position.
sum + (delta / (delta r squared + 2))].
acceleration := velocity * -0.0001 + acceleration.
velocity := velocity + (acceleration * 10) .
position := position + velocity.
self position: position rounded
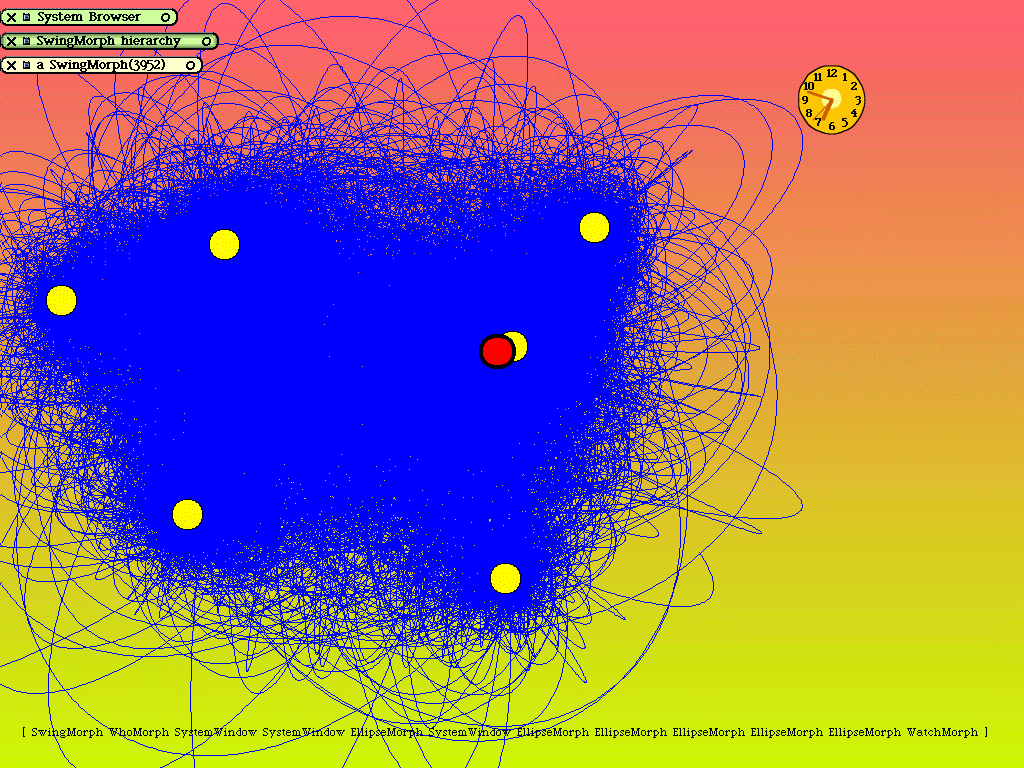
I added a few ellipses to my desktop and then one of my new active variation. (I called it a SwingMorph because that's what the dangling arm of the toy did.) It moved. In fact it moved too much. If it swung directly over a magnet it would pick up a kick from delta r approaching zero and go flying off the screen. I added a few pixels of ever-present spacing, much like that in the toy itself. (The magnets never touched.) The morph still accumulated energy. I added a little bit of velocity dependent resistance (like air resistance) to make it stable, though still chaotic, in the long term.
I used floating point for all my numbers. These feed deep into the Morphic system which is used to working with integers. All worked fine except for one thing: the refresh region bounding box calculation was sometimes off by one. This meant that my morph would leave little trails of incorrectly refreshed pixel debris. Yuck.
I decided to keep my own precision position and send a rounded copy of that into Morphic. This cleaned up the display but interfered with manual placement of the morph. Hmmm. I'd better back this last change out and fix Morphic.
I kind of missed the debris trail's arcs and swoops. Looking a little further into Morphic I discovered that every morph could draw. (See TurtleGraphics). I told my morph to lower its pen. Bingo. A beautiful drawing of the trajectory. I let it run all night and wrote it up in the morning. Here is the source for the whole morph.